概 要
本稿では垜術問題を取り上げる。安井金比羅宮奉納算額（天保12年（1841）奉納）中の第4問は、まさにその垜術問題である。その垜術とはいかなる術か。このことは、本文展開の中で詳細に述べるとして、ここでは先ず、第4問の漢文記述解読を通して問題の数学内容を明らかにする。次にその数学問題を、筆者も学んだ洋算で解いてみて、問題のレベルを探ってみる。最後に問題レベルを踏まえた上で、小学校高学年の児童を対象にした教材化案を提案する。
１．垜術とは何か
数多ある和算の術の一つに垜術がある。垜というのは、下図のように積み重ねるという意味である。そのいろいろな積み重ね方は、日常生活上にも存在する。和菓子屋さんの店先では、下記のように規則正しく積み重ねられた和菓子の陳列をよく見かけるし。高価な化粧品の箱を規則正しくウィンドゥ一杯に積み重ねたデパート風景もよく見かける。そんな風景を目にした時、先ず印象付けられるのは。美しいという感覚だろう。次に湧き出てくるのは、いったい全部でいくつ積み重ねているのか、重ねの構造がどうなのかとの素朴な思いであろう。
〔四角垜
（平方衰垜）〕
〔三角垜
（三角衰垜）〕
こんな素朴さを出発点に、積み重ねの構造と総量を数列として研究対象としたのが垜術である。江戸期経済の中心にあった米、その俵の安定した積み重ね方と総量が垜術の出発点であったと思われる。
２．安井金比羅宮算題四季詠四月問題
（１）原文の解読及び現代訳
③現代訳 ②書き下ろし文 ①原 文
（２）難解語句の解説
六角垜（ろっかくだ）：
垜とは積み上げるとの意味であることから、例えばコインや球を六角錐のように積み上げたものを六角垜という。下記図は、どちらも六角垜であるが、問題文中に如図(図の如く)とあることから、下記左の積みあげ方が問題文に合った積みあげ方であり、下記右の積みあげ方ではない。因みにピラミッドのように積み上げたものは、四角垜という。
底子（ていし）：
底辺は左下の場合は３で、右下の場合は５である。即ち底辺に並ぶ一辺の数のこと。
〔二つの六角垜〕
-
- 〔問題にあった積みあげ方〕
-
- 〔問題に合わない積みあげ方〕
３．問題の解答
〔現代訳〕
❶底子４までのモデルをそれぞれ作る。
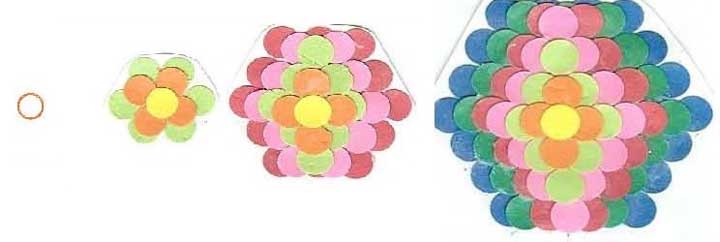
底子１ 底子２ 底子３ 底子４
❷底子４までののモデルをそれぞれｎ解体して順序よく整理する。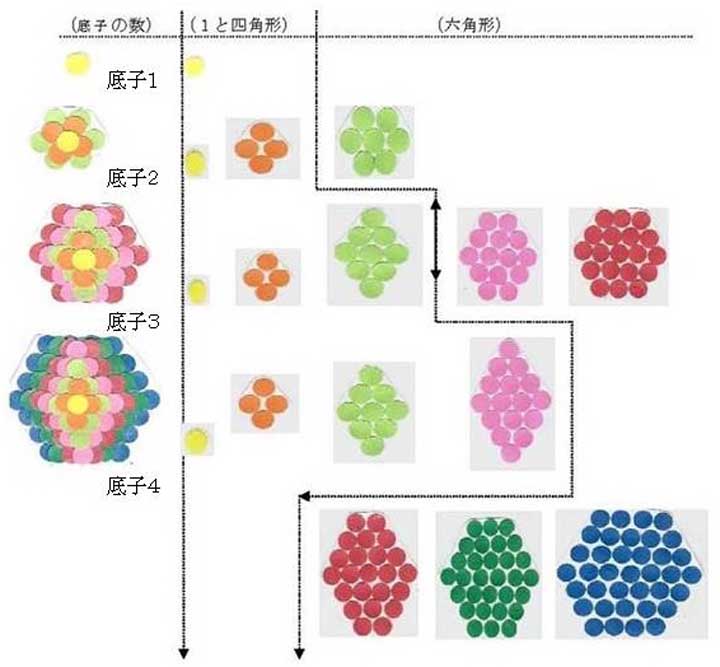
❸ ❷の具体を数値に置き換え,底子5の場合の数値を推定する。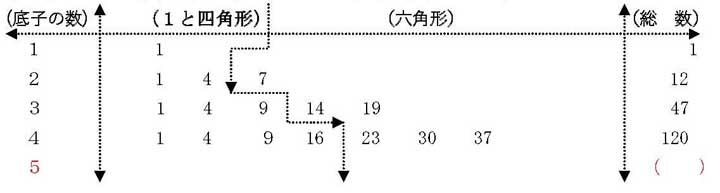
❹ 規則性を見つけ，必要な公式を適用して問題解決をはかる。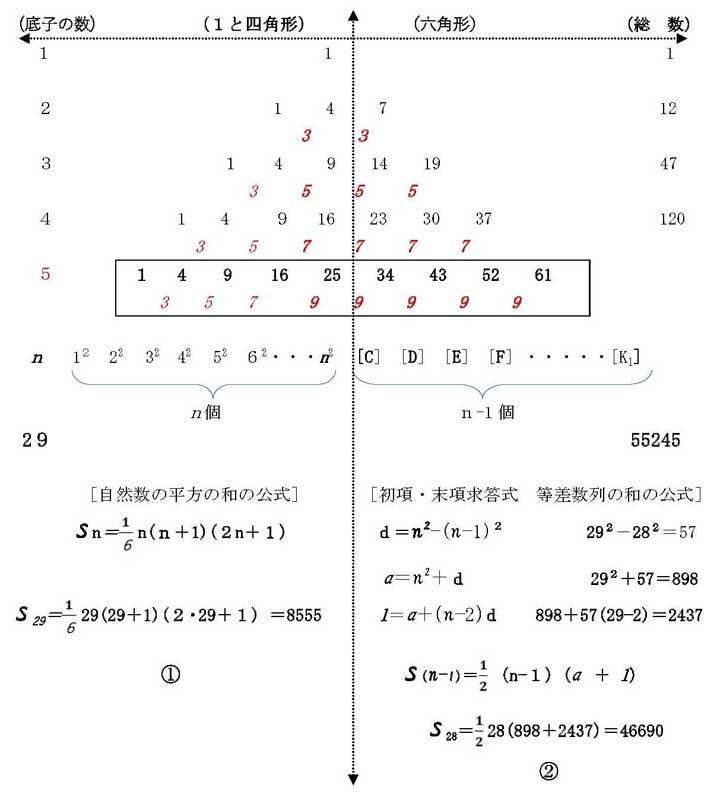
①+②＝8555+46690＝55245
答曰 団子の総数55245の場合は底子29となる
注１：
問題文中の如図（図の如く）の具体は、確かに２頁左図である。しかし、団子（球）は図の如く積み上げられない。団子（球）のような具体を積みあげられたのは、同頁右図である。左図の場合、これはどう見ても団子ではなく、極端な言い方をすれば煎餅であろう。その意味で、この問題は問題文全体に矛盾はあるのだが、ここではそのことの問題化は差し控えたい。
４．問題レベルの確認と小学生への教材化
（１）問題レベルの確認
本教材をそのまま活用できるのは、「数列（高校数学B）」を学び終えた高校生だろう。なぜなら、「自然数の平方の和の公式」や「等差数列の和の公式」並びに「初・末項求答式」を学び終えていないと、団子総数が55245個となる場合の底子の求答に、膨大な時間的ロスが生じるからである。それでも根気と呑気さえあればできないことはないが、現状はそんなロスタイムを許さない。公式の理解と活用は、求答が極めて容易になるに留まらず、数学の威力という点からも、重要な意味を持つ。
（２）小学生（高学年）への教材化
しかしながら、小学6年生にはここで用いる公式の理解と活用まで要求できない。またすべきでもない。子どもの発達段階を踏まえて、次に2点の成就が重要となる。即ち
①「伝統文化である和算問題に挑戦している」との意識
②「難問に挑んで頑張り抜いたら出来た」との達成感
である。したがって、小学生への教材化は、上記2点が充満するレベルの問題にすべきであろう。例えば、次頁〔教材化案問題〕に示した問題はどうだろうか。
５．教材化確定に向けた授業
（１）教材授業化の目的
次の五項目の数学的活動過程を、子どもに体験させることを目的としたい。
⓵問題解決に向けて、単純な場合の具体モデルを作る。
⓶モデルを解体して整理し、具体モデルから数値モデルに変換する。
⓷変換した数値モデルから、その中に潜む規則性を発見する。
⓸発見した規則性にもとづき、提示問題の解決を図る。
⓹解決の結果が正しかったかどうかを、具体モデルに戻って確認する。
（底子５のモデルは、指導者が事前に作っておくもよし。）
上記⓵～⓸の過程は、具体から抽象に向けて、「数学の学習水準（ステ―ジ）」を次々と上昇させる学習場面となる。次の学習水準への上昇の様相は、スパイラルではなくジャンプ（飛躍）によることに注意したい。もしその体験が子どもになければ、当然、指導者の指導事項となる。⓹も、抽象化して得た結論の良否を具体でもって再確認すべく、ジャンプでもって、具体世界に戻らねばならない重要な水準の飛躍である。
（２）指導計画（全４時間）
第１次 問題の題意を掴む
第１時 原典に触れ、解読過程を通して問題の題意を掴む
第２次 問題解決に挑む
第２時 問題解決に向けて、簡単な場合の具体モデルを作る（底子２~４の場合）。
第３・４時
＊具体モデルから数値モデルへの変換とそこからの規則性の発見。
＊規則性にもとづき、底子５の場合の総数を求め、総数の是非を具体モデル
で確かめる。
家庭学習 問題解決の過程を振り返りまとめる。
（３）授業の実際
第１時 原文に挑戦する 
子たちは、漢文ばかりで記された問題に直面して、「エエッ、これ算数の問題？」とばかり、仰天の声を上げる。その出会いを大事にして、原文解読に挑戦させたい。ところどころ知っている漢字はあっても、文章としては解読できない。それでいいのである。解読させることが目的ではない。興味関心を深化させることが目的だからである。
頃を見計らい、〔現代訳〕文を提示する。〔問題原文〕に比べて、だんぜん読み下しが容易になる。指導者の範読と文章が一致することから、子どもたちが後を追って声を上げる。何度か繰り返しているうちに、子どもの心中に難解語句が芽生え始める。
子どもの中から、「六角垜って、何ですか。」、「底子って何ですか。」等の声が上がり出したら。第1時限の授業としては大成功。
興味・関心が深まったと判断したところで、〔教材化案問題〕を提示。
第２時 問題解決に向けて、簡単な場合の具体モデルを作る（底子２~４の場合）。
〔教材化案問題〕
〔底本３の場合〕
今図のように仏前にお供えする団子がある。底子が５個になる場合の六角垜（右図は底子３の場合の六角垜）に積みあげた団子の総数を求めよ。
（底子及び六角垜は、出典の原型をとどめるための用語としてそのまま提示する。しかし、それらの解説は指導者に委ねる。）
〔子どもに作らせたい六角垜モデル〕
（底子１） （底子２） （底子３） （底子４）
第２時 具体モデルを解体して整理し、数値モデルに変換する。 〔具体モデルの解体図〕
〔具体モデルの解体図〕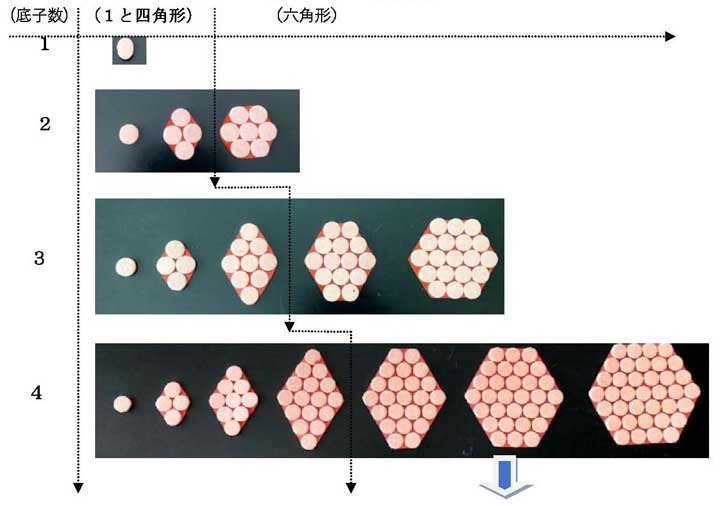
〔数値モデル その１〕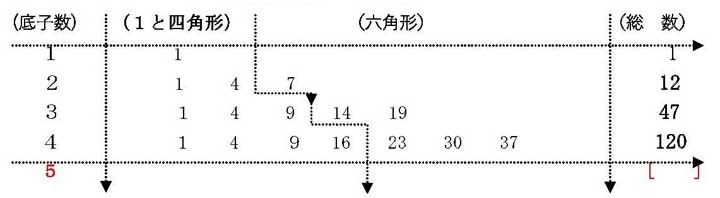
第３時 数値モデルから規則性に着目して、問題解決方法を探る。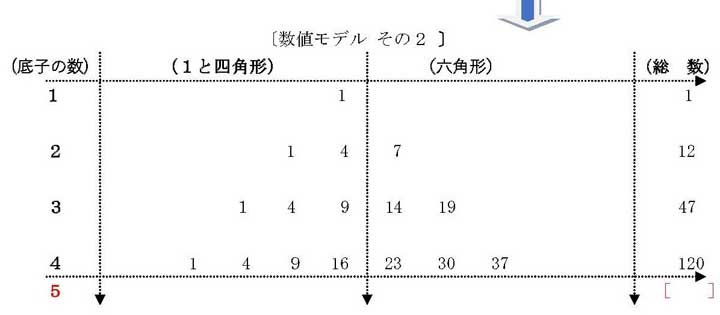
第４時 規則性にもとづき、底子５の場合の総数を求める。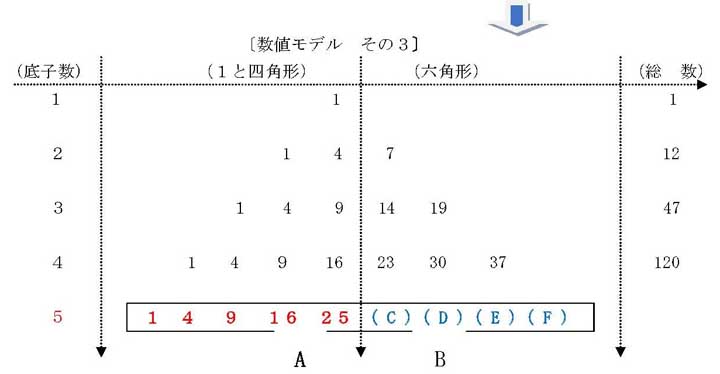
【重要な学習場面－１－】
T：この表（その２）をよく見て、底子５の場合のAの部分にどんな数字が並ぶかを見つけてほしい。:
C：１、 ４、 ９、 １６、 ２５ です。（根拠の説明は略）
T：マッチ，グーだ。
T：では、Aに５つ並ぶんだったら、Bにいくつ並ぶか。
C：4つ並びます。（根拠の説明は略）
T：マッチ，グーだ。
T：では、（C）の数字はいくつになるかな。
C：ウ、ムムム、ムっ？
T：この数値モデルの表（その３）の中から規則性を見つけて、考えてほしい。
〔数値モデル その４〕
【重要な学習場面－２ー】
C：１６と２５の差は9だから、C ＝25＋９＝３４、D=３４+９=４３、E＝５２、F=６１
AとBを加えると総数が出てきます。 総数 A+B=５５＋１９０=２４５。
【重要な学習場面－３―】
T：それが正しいかどうか、総数の是非を底子５の 〔底子５の六角垜〕のモデル〕
の具体モデル（指導者が用意）で確かめよう。
〔底子５モデルの解体図〕
〔底子５モデルの解体図Ｂ〕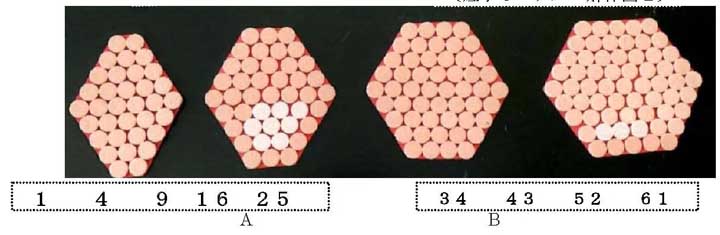
C：確かめました。途中の数字も全て同じで、総で、マッチ、グーです。
答日 底子５の場合の団子の総数は２４５個
6．本稿のまとめ
算額問題を小学校で教材化することについては、小学校教員間で異論、反論のあることは承知している。しかし、小学校も六年生になれば、教材化した素材をもとに適切な指導を加味することによって、授業化が可能になることもまた事実である。そして、その適切な指導の具体を、本稿 ５．教材化確定に向けた授業 で展開した。筆者らの著書『和算 算額問題の教材化』注 でもそのことを記したが、本稿は新学習指導要領の理念に沿って再編し直したものである。５の（１）教材授業化の目的 に記した五つの目的、即ち
⓵問題解決向けて、単純な場合の具体モデルを作る。
⓶モデルを解体して整理し、具体モデルから数値モデルに変換する。
⓷変換した数値モデルから、その中に潜む規則性を発見する。
⓸発見した規則性にもとづき、提示問題の解決を図る。
⓹解決の結果が正しかったかどうかを、具体モデルに戻って確認する。
は、教材化案として示した素材をもとに、授業を通して育てたい「新要領の子ども像」そのものである。よってその具現化に向けては、教科書教材だけに頼らず、教材収集の範囲を和算・算額領域にまでひろめていただければ幸いである。
【引１】
平野年光著『和算・算額問題の教材化』62頁東洋館出版社 2014（平成26年）
[参考文献]
-
安藤三央「ある問題との遭遇から深い理解にたどり着くまでの心的過程」『和算・算額問題の教材化』86～104頁 東洋館出版社 2014（平成26年）
-
平野年光「第1章 算額問題の教材化」『和算・算額問題の教材化』4～11頁 東洋館出版社 2014（平成26年）
-
小寺 裕『日本の算数 和算って，なあに？』 株式会社少年写真新聞社2015（平成27年）
-
神田 裕「算数・数学科における問題作りー発展的な扱いによる指導について・算額づくりへの示唆―」『和文化数学第3号』35～47頁 NPO法人和算問題教材化研究会編 2019（令和元年）
-
山本景一・大林正法「子どもたちと楽しむ和算問題作り」『教育実践研究第2号』43～55頁 桃山学院教育大学教育大学紀要編集委員会 2020（令和2年）
-
西川恭一・綿谷徳子「和算問題の教材化―問題作りを生かした取り組み その１－」『和文化数学第4号』36～46頁 NPO法人和算問題教材化研究会編 2020（令和2年）